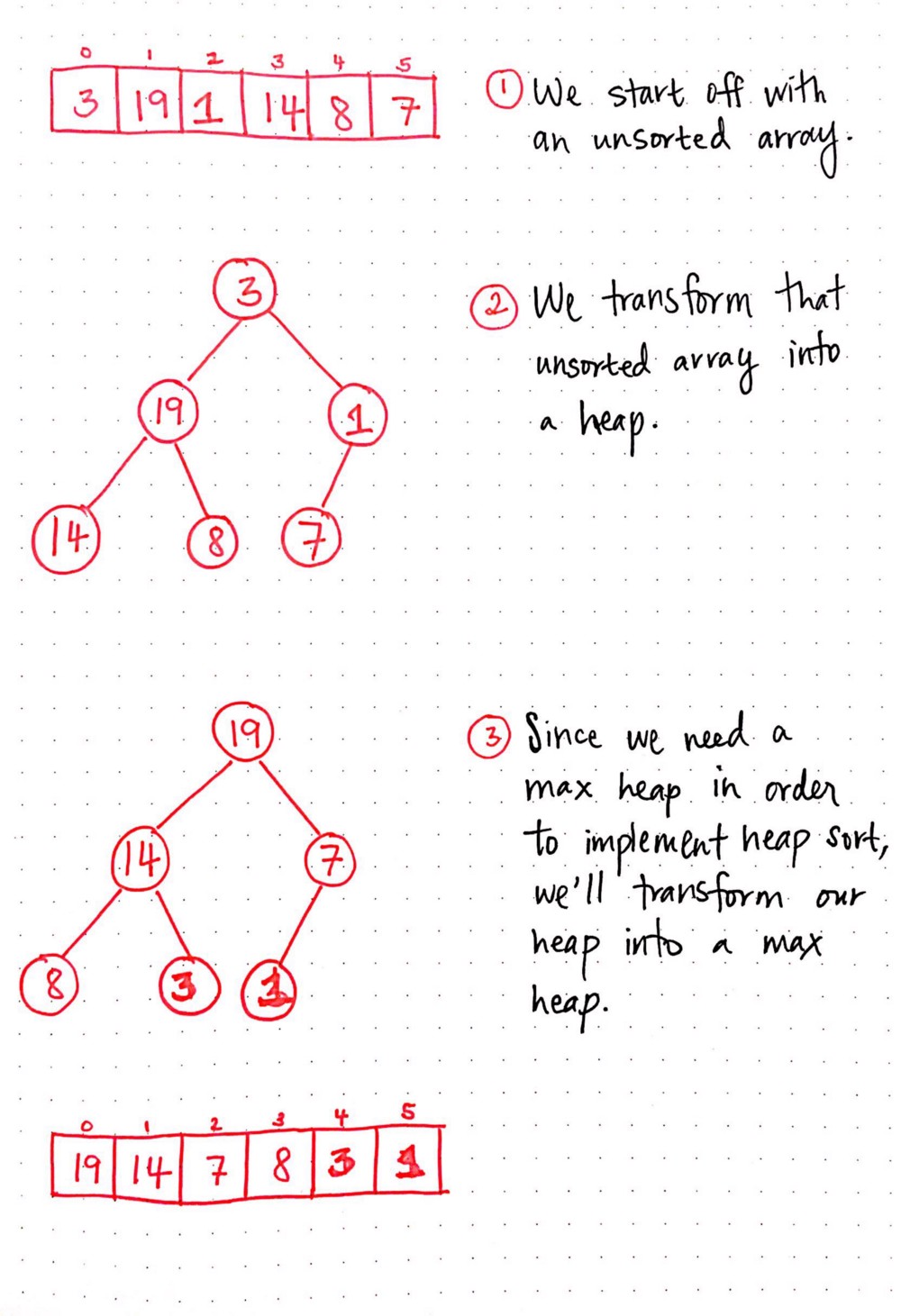
Thinking:
buildMaxHeap(arr)
1 loop through all non-leaf node => Math.floor(arr.length/2-1) from last non-leaf node to first non-leaf node 2 compare that node with its 2 children to find out the largest number by heapify method
heapify(arr,i)
1 get three dots’ index or values: current non-leaf node: arr[i], left child node index: 2i+1 right child node index:2i+2
2 firstly, compare left child node with current non-leaf node 3 then, compare right child node with current non-leaf node 4 if the temp max index has changed, we need to swap the value between those nodes, and also need to call heapify(arr, max) again, to re-sort the remaining nodes, to find out if there is another max node exists
heapSort(arr)
the main function of this method is to swap the largest node value to the end of the arr and then excludes the sorted largest values from the array, re-sort the rest unsorted array to find out a new largest node value again 1 call buildMaxHeap(arr,heapSize) to initialize the correct heap in the first time 2 loop through the array from end to start, swap the arr[arr_length-1] with the arr[0], put the largest node value to the end of the array 3 reduce the array length by one to exclude the sorted values 4 since currently the heap is in the correct structure,(from top to bottom, from left to right is sorted from large values to small values), so we only need to call heapify(arr, 0, heapSize) with second parameter ‘0’, this means we only need to sort the topped node to find out the largest value in the array, no need to sort the largest value from the non-leaf node from the bottom of the tree again. 5 that’s it~!
let arr = [3, 5, 14, 8, 20]
const buildMaxHeap = (arr, heapSize) => {
//从非叶子节点开始对每一组堆进行排序,保证 parent node 值最大
for (let i = Math.floor(heapSize / 2 - 1); i >= 0; i--) {
heapify(arr, i, heapSize)
}
}
// recursion happened here
const heapify = (arr, i, heapSize) => {
let leftIndex = 2 * i + 1
let rightIndex = 2 * i + 2
let tempMaxIndex = i
//...我彻底忘掉了控制原数组长度-> 因为之后我们需要移除最大顶点值,每移除一个最大顶点值就需要数组减去一个元素长度
// 三目运算符不能随便用!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!会出bug, 没 debugger 过,不打算细究,就是测试出来不能随便用三目运算符
if (leftIndex < heapSize && arr[leftIndex] > arr[tempMaxIndex]) tempMaxIndex = leftIndex
if (rightIndex < heapSize && arr[rightIndex] > arr[tempMaxIndex]) tempMaxIndex = rightIndex
// 忘了运行swap需要一个条件,就是 tempMaxIndex !== i 的时候才需要swap
// 因为如果 最大顶点值就是 当前non-leaf node的话,那没必要swap啊
if (tempMaxIndex !== i) {
swap(arr, tempMaxIndex, i)
heapify(arr, tempMaxIndex, heapSize)
}
}
const swap = (arr, one, two) => {
// temp <- arr[one] <- arr[two] <- temp
let temp = arr[one]
arr[one] = arr[two]
arr[two] = temp
}
const heapSort = (arr) => {
//因为arr_length需要在本方法内递减才能剔除掉顶点值,所以在这里 跟全局变量arr_length关联上
let heapSize = arr.length
buildMaxHeap(arr, heapSize)
for (let k = arr.length - 1; k > 0; k--) {
swap(arr, 0, k)
heapSize--
heapify(arr, 0, heapSize)
}
}
heapSort(arr)
console.log(arr)